Ground Rules by John Cadick: Symmetrical Components

By John Cadick, P.E., Cadick Corporation

Table of Contents
Introduction
The Sequence Quantities
The Sequence Networks
System Short Circuits
Modeling Short Circuits

Introduction (Back to top)
The method of symmetrical components is a mathematical technique that allows the engineer to solve unbalanced systems using balanced techniques. Developed by C. Fortescue and presented in an AIEE paper in 1917, the method allows the development of sets of balanced phasors, which can then be combined to solve the original system of unbalanced phasors.

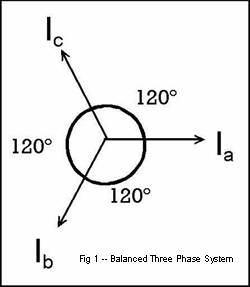
Figure 1 illustrates a balanced, three-phase system of phasors. Note that each of the three phasors is equal in magnitude and displaced by 120 degrees from the others. Further, the direction of positive rotation is counterclockwise. Such a diagram might represent the three phase currents in a normally operating power system.

Figure 2, on the other hand, shows an unbalanced system, where the three-phasor magnitudes are not equal, |I_a||I_b||I_c| and the three phase angles are not necessarily 120 degrees. The phasors labeled as the Original System in Figure 2 are typical of the currents in a three phase system with a short circuit to ground on phase A.

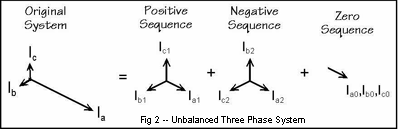
The concepts illustrated in Figure 2 are stated mathematically in Equations (1), (2), and (3).

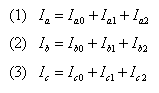
If the vector operator ‘a' is defined as:

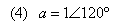
then:

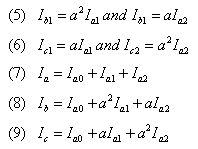
The Sequence Quantities (Back to top)
From Equations (7), (8), and (9) you can see that each phase wire will have its own, independent sequence currents flowing in it. The A phase wire, for example, will have its own positive sequence current (I_a1), negative sequence current (I_a2), and zero sequence current (I_a0). The total current in any phase wire is then expressed as the sum of the three sequence components.

It is especially important to note that, even though the total current in any given phase may be equal to zero, the individual sequences are not necessarily equal to zero. In a single phase fault, for example, I_b and I_c are both zero; however, the phase B and phase C sequence components (I_b1, I_b2, I_b0, I_c1, _Ic2, I_c0) are not zero.

Equations (7), (8), and (9) can be solved for the sequence components as shown in Equations (10), (11), and (12). You can see that for any given set of phasors (I_a, I_b, I_c), there exist three unique sequence phasors (I_a0, I_a1, I_a2). Equations (13), (14), and (15) show the same solution applied to the power system voltages.

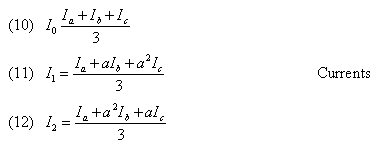
and

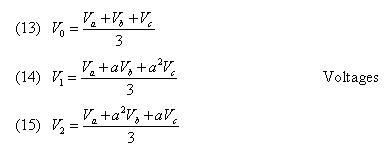
Notice also, that by convention, the phase subscript is dropped. Thus I_a1 becomes I₁. This causes no confusion since the convention is generally applied throughout the industry.

The Sequence Networks (Back to top)

1. For any three-phase system, three sets of independent sequence components can be derived for both voltage and current.
   
2. Since the three sequence components are independent, we may infer that each sequence current flows in a unique network creating each sequence voltage.

Taken together, these two points imply the existence of sequence impedance networks as shown in Figure 3. Each sequence network represents the entire power system reduced to a single impedance. The N_x terminals are the neutral or return terminals for each network. For a short circuit study, the F_x terminals represent the assumed point of the short circuit.

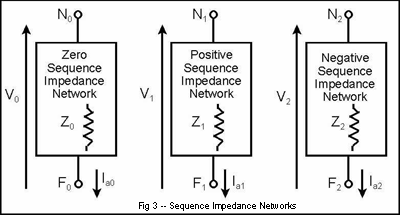
As soon as the engineer has developed the three sequence impedance networks, the analysis of the system may proceed.

System Short Circuits (Back to top)
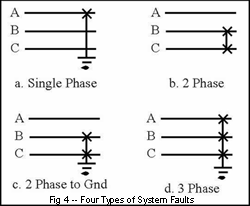
Four types of short circuits may occur in a power system. The basic configuration of each short circuit is shown in Figure 4. Note that the nature of each type of short circuit creates certain mathematical boundary conditions, which are listed in Table 1. These boundary conditions are particularly useful since they can be used to determine how to model a faulted system with the sequence impedance networks.

Modeling Short Circuits (Back to top)
The model for a single-phase short circuit will be developed in this paper. The three other types of connections may be developed using similar methods. For a single-phase short circuit, first we consider the current boundary conditions which state that I_b=I_c=0.

Inserting the boundary conditions into equations (10), (11), and (12) results in:

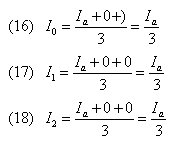
The voltage boundary condition is that V_a=0. Substituting this condition into equations (13), (14), and (15) and adding the three gives Equation (19).

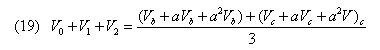
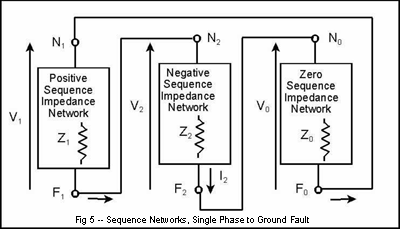
Equations (16), (17), (18), and (19) may be seen as statements of Kirchoff's laws — the sum of the voltage drops around a series circuit is equal to zero and the currents in a series circuit are equal throughout. Thus Figure 5 illustrates the proper connection for a single phase to ground fault.

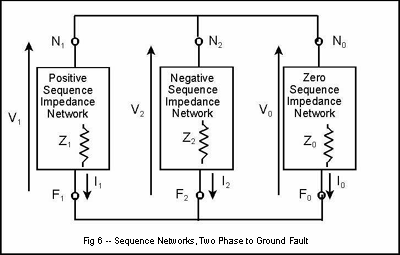
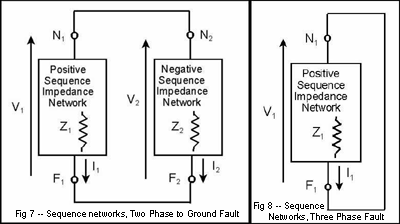
By similar reasoning, Figures 6, 7, and 8 can be shown to the be correct circuits for two phase to ground, two phase, and three phase short circuits, respectively.

---

A registered professional engineer, John Cadick has specialized for three decades in electrical engineering, training, and management. In 1986 he created Cadick Professional Services (forerunner to the present-day Cadick Corporation), a consulting firm in Garland, Texas. His firm specializes in electrical engineering and training, working extensively in the areas of power system design and engineering studies, condition based maintenance programs, and electrical safety. Prior to the creation of Cadick Corporation, John held a number of technical and managerial positions with electric utilities, electrical testing firms, and consulting firms. Mr. Cadick is a widely published author of numerous articles and technical papers. He is the author of the Electrical Safety Handbook as well as Cables and Wiring. His expertise in electrical engineering as well as electrical maintenance and testing coupled with his extensive experience in the electrical power industry makes Mr. Cadick a highly respected and sought after consultant in the industry. (Back to top)