The Theory of Power Factor Testing — Part 1
By Rick Gaskey, AVO International
Why do we want to see power factors in the 0.0% to 2.0% range (0.0 to 0.02) when analyzing from an electrical testing point of view? Why do we want to see power factors in the 90% to 100% (0.9 to 1.0) range when analyzing from a power generation point of view? No one usually asks these questions since they are questions that many people can not answer. However, once an explanation is given and you are aware of the correlation between the two, it should help give you a better overall understanding of power factor.
Electrical Theory
The answer lies within basic electrical theory. First, let's look at the power generation point-of-view. As stated, we already know to desire a high power factor. The closer to 100%, the more "efficient" the generating system. The easiest way of approaching this is by using the power triangle. We know about electricity two things.
The only things we have to represent electricity are numbers, but the power triangle gives us another visual means of representing electrical quantities.
Power Triangle
The power triangle appears like this:
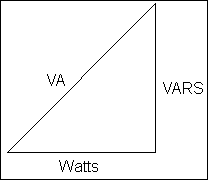
Let's give a quick review of resistive, reactive, and total power — the parameters of the power triangle. Resistive power is the desired component and is considered the DC portion of the power triangle. In a nonprofessional's terms, its unit is Watts and it is what we use for everyday electrical energy.
Reactive Power
Reactive power is the unwanted portion of the power triangle (power generation being the consideration) and is the AC component of the power triangle. The units are VARS, which stands for volt-amps of reactance. A system introduces reactive power whenever there is a rotating sinusoidal source delivering energy. "Total" reactive power is either capacitive or inductive but not both. Why? Because mathematically, capacitive reactance is a negative parameter while inductive reactance is a positive parameter, therefore, the two cancel out each other. If there is more inductive reactance than capacitive reactance, the circuit is inductive with a "lagging" power factor. The situation is vice-versa for a circuit that contains more capacitive reactance than inductive reactance. The circuit would then be capacitive with a "leading" power factor. When we use the terms leading and lagging, we mean the current waveform is either leading or lagging the voltage waveform. Ideally, to obtain a power factor of 100% (1.0), the voltage and current waveform would need to be exactly in phase.
Total Power
The last component in the power triangle left to discuss is total power. The units for total power are VA, which stands for volt-amps. Volt-amps are the total apparent power of the system with its value being the product of the system volts and the system amps. When viewing the power triangle, one can see that it is a right triangle, thus Pythagorean's Theorem must hold true. This in turn defines total power as being equal to the square root of the sum of the reactive power squared and the resistive power squared, as given by the formula below:

Remembering basic electrical theory, we know power factor = cosine theta. We also know cosine theta = adjacent / hypotenuse by trigonometric definition. From this, it is easy to see that power factor = Watts / VA, or the ratio of true to apparent power. There are many ways to define power factor; those previously mentioned are two of the most common.
Generation Viewpoint
When considering power factor from a power generation point of view, it is important to understand that generators are not rated in megawatts (MW), but are instead rated in mega-volt-amps (MVA). This is contrary to popular belief. As stated previously, watts are the portion of the power triangle used for energy consumption. This is referred to as "true power". The volt-amp portion of the power triangle (hypotenuse) shows how hard a generator must work in order to produce the relative amount of watts. As stated above, volt-amps are referred to as "apparent power". Utilities concern themselves with this for several reasons. One of the main reasons is the heating effect of the current on the generator insulation.
For example, if a generator has to produce 100 MVA to get 90 MW worth of usable power (this will give a single phase power factor of 0.9), it will obviously have to create more total current than it would if the power factor was higher, such as 0.95. In other words, if the power factor were higher, the generator would not have to produce 100 MVA to get 90 MW worth of power. This would give a smaller magnitude of total current. One must remember that current is the source of heat, and heat is the main cause of insulation deterioration.
Another cause for concern would be capacity. If a generator was rated at 100 MVA, it could deliver 100 MW with a power factor of 1.0 (practically unachievable). With a power factor of 0.95, it could deliver 95 MW (for a single-phase system), thus losing 5 MW of its capacity to generate revenue. In other words, that's 5 MW of power capacity for which the utility can not be paid.
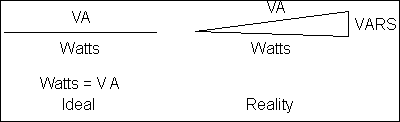
There are other ways of looking at the power factor model from a power generation point-of-view. Although it is sometimes used for voltage control, reactive power (the vertical component of the triangle) is somewhat unwanted. The ideal model would simply be a straight horizontal line as shown below. The straight horizontal line would represent a totally resistive system or a system where the inductive reactance and capacitive reactance are exactly equal. However, in reality the model will look more like the triangle shown below. This only makes sense, since the cosine of zero degrees is equal to 1.0. The smaller the angle, the better the power factor.
This is the first part of a two part series. The second part will discuss the impact of power factor on electrical testing.
About the author
Rick Gaskey is an Applications Engineer for AVO International.
